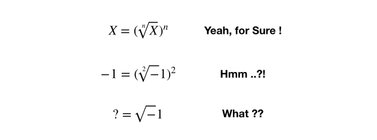THE NUMBERS: That's what it's all about

Mathematicians like numbers, no surprise in that. Because what would Math be without the numbers.

Every knowledge established by science, begins with knowing about the numbers. And yes, certain types of numbers can be confusing, the first time you encounter them. To start with, the symbols being used can be intimidating. But behind the strangely looking signs and operators lies an equally challenging interpretation. How do we represent nothing. How do we represent infinity. And when numbers start having infinite amount of decimals, does that mean that the number is not exactly defined anymore. For instance; how can a number having infinite number of decimals correspond to a distance in the real world between object A and object B … that we know is not infinite, and actually very concrete.

Nowadays, numbers are in most situations intuitively understood, for all of us.

But if you are a Mathematician, you would say that there are different kinds of numbers, and then you would also know that is has take many thousand years to "discover" them all.

Along the way, by reasons of the history behind their discovery, they have been given strange names like integers, irrational numbers and transcendental numbers, referring to the characteristics of the numbers that belong to these classes.. 

Don't let these exotic names confuse you. In reality they are all just real numbers, some of them with decimals, and some of them even with infinite number of decimals.

The number class that is somewhat different from the rest, is the one called complex numbers.

This article is about this class of numbers. The objective is to help you understand where they originate from, and why they are important.

And hopefully you will then understand that they are as central to math as plus, minus, division and multiplication. And most importantly; complex numbers are not a human invention. Complex numbers were brought to life, the day people moved on from only doing counting, and started writing equations .

On top of everything else, you will also learn that - almost as by a magical touch - these complex numbers can be visualized in a very intuitive way, and that the visual representation bears with it important semantic information about the equations and the solution space that they are part of.

Let's start with a little example.  

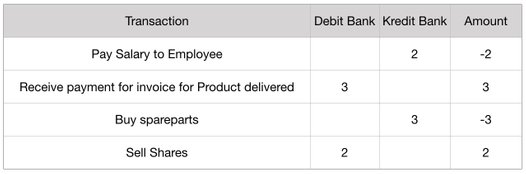
Imagine that you have a company, and that this company's bank account, each month, makes 4 types of transactions, as shown in the table.

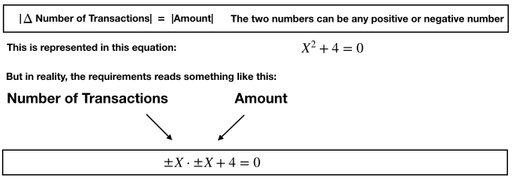
The company now receives 4 (e.g. dollar) from an investor. And this investor puts forward the condition that these 4 dollar must be transformed into initiatives - i.e. bank transaction changes - that balances this amount. And with one an additional requirement: the changes in the number of transactions must match the amount of money being transferred in the transaction. What this means is that if a transaction changes the account by the amount of 2 or minus 2, then you must also do 2 of them. And if the transaction amount is 3 or minus 3, you must do 3 of them and so forth.

After the accountant has done the math, the result is clear. There are only 2 valid options:

A) Hire 2 additional employees -> increase salary pay, delta = 2 x -2 = -4 

B) Reduce the number of shares sold ->decrease in income, delta = -2 x 2 = -4

Both of these fulfills the requirements of the investor, and amounts in total to the 4 dollars that was infused into the company; spending increased with 4 dollars.

But while doing the calculations, the accountant came across an insufficiency of the mathematical tools and formulas he was using. The equation he needed solving involved looking for the squareroot of the negative number -4. And that cannot be solved through traditional, basic school algebra.

The root of the problem is that when you multiply X with X, the result will always be positive. 2 x 2 = 4 and -2 x -2 = 4. And if you wanted to allow for the two variables to have opposite signs, you would have to call the one X and the other Y, but that would only complicate things further, because of their required equal size (X = Y), as demanded by the investor.

Let's briefly dvelve on this. The issue here does not come from numbers or minus and plus signs. The issue is inherent in the mathematical construction that we call X to the power of N, and the way that it is calculated - because this does not support calculating with different signs of the X-elements in the expression!

The solution to this, is to understand that X to the power of N has to be understood differently than what we are used to, namely that we have to allow for the sign of X to be arbitrary for each of the elements (i.e. X's) being multiplied. And the result of the multiplication will then be either 100% negative or 100% positive. 

The trouble arise when the result of X to the power of N is expected to be negative.

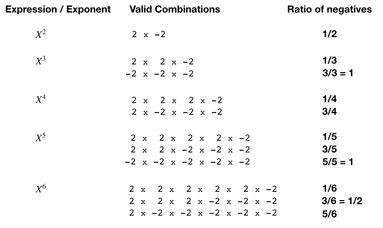
Elaborating the example about to more than a 2 dimensional puzzle - writing all possible combinations of plus (2) and minus (-2) elements for N between 2 and 6 - where the product has to be negative, like -4 in the original example - we realize that as N increases, the number of combinations grows. And the ratio/fraction of -2 of the total number of elements for each of the equations - for the equation to be valid - changes accordingly.

(notice: the examples in the illustration sticks to the root number =2, just for convenience, but the principle can be used for all other roots also).

Let's pause here for a moment. Have a look at the illustration showing the number of combinations for N between 2 and 6. Please notice that the fraction is NOT saying anything about the sum of the calculation. The fraction represents the fraction of the elements that has a minus sign. For instance cubic X = -8, has two solutions. X = -2 (this is the basic stuff saying that all the 3 elements are the same, and equal to -2) or X = 1/3 of the elements is negative 2 (this is the good stuff; what this says is that 1/3 of the elements is -2 and 2/3 of the elements are 2).

2 x 2 x -2 = -8. 

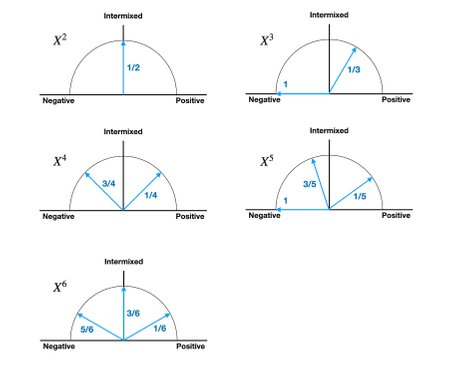
Now let's for the fun if it convert these Power N: 2-6 results into 5 graphics. These graphics are to be viewed as a meter (a scale) where the negative/positive ratio is represented by the angle of the arrow. If the arrow is 90 degrees, i.e. pointing directly upwards, this is representing the situation with a 50/50 negative/positive ratio. If the ratio is 100% negative, meaning that all the elements are -2, the arrow is pointing straight to the left. I hope you understand this illustration methodology. The angle of the line indicates the balance between positive elements and negative elements!

The larger the negative fraction, the more the arrow points to the left.

The larger the positive fraction, the more the arrow points to the right.

So far so good. Now that we have a visual representation of what is happening, let's look at this in a more mathematical way.

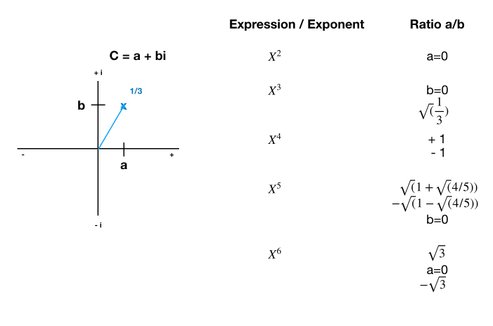
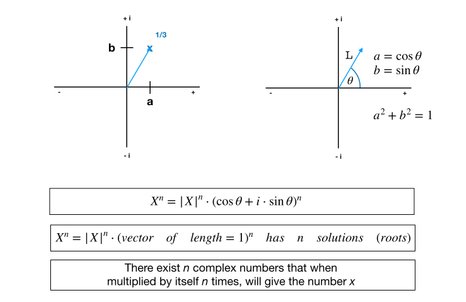
Inspired by the graphical representation, let's pretend that X can be represented as a number in a two-dimensional coordinate system. In this 2-axis system, the first coordinate would indicate the line's projection on the horisontal axis, and the second coordinate would indicate the line's projection on the vertical axis, as shown in the illustration. This would mean that x = a + bi, where a and b are both real numbers, a is representing the ordinary dimension and i is representing the perpendicular "intermixed" dimension.

Following this line of reasoning, reveals something interesting. If (a+bi) squared is to result in a real, 100% positive or 100% negative number - and it must, because these are the only two options that exists in the all of the various combinations mentioned above - then i squared must be equal -1. So if we want to represent complex numbers as x = a + bi, then this is a consequence that we will have to accept - that i times i = -1. And do you know what. It really, really doesn't sound that strange after all. Because what this is saying is, that if you intermix 1 with -1 and multiply them, you'll get -1. Do you see it? 1 x -1 = -1. It's simple to grasp, as long as you remember that i means "intermixed".

And now to another interesting finding. If (a+bi) squared is to support that x = a + bi can be intermixed in a 50/50 negative/positive factorization, the variable a must be equal to zero (because 50/50 split means that the meter is pointing straight up - 90 degrees vertically - with no tilt to the left or right).

Comparing this with our graphical representation, we can see that there is a match between the two models - the graphical meter and the a + bi representation. 

Ok, maybe this was just a coincidence. Let's try to do the same simulation with X to the power of 3 also, to see if that will work equally well.  

When doing the math on the cubic version, the first finding we get is that the a/b ratio matches an angle of 60 degrees. On the graphical representation, the negative ratio was listed as 1/3. And 100% negative = 180 degrees, which means that 1/3 of 180 = 60. So the number 60 is actually equal to the ratio 1/3 (1 negative element out of 3 elements). 

Our a + bi model is starting to look good - really good. 

Now that the angle matches in the two models, let's get more ambitious. Instead of thinking of a + bi as a point, let's instead think of it as an arrow pointing from 0,0 to a,b. (this arrow, in mathematical terminology is called a vector).

As the math shows, using the Pythagorean theorem, what we get is a vector of length |X| and an angle matching the negative-ratio.

And if we look isolated on the value |X| separating the koordinates a and b, then we can get to a very simple expression of X, where the vector is of length = 1.

(this will be very useful in just a moment).  

Continuing on with the powers 4, 5 and 6, and performing the same algebraic exercise, we get a/b results that exactly matches the "meter representation"
(I'll leave it to you to test that this is actually true, using the trigonometric functions). 

What we have learned is, that the vector representation can be used as the general method, and therefore we'll stick to this from now on. But going forward, please always remember where this came from, and what the vector direction actually indicates - namely the ratio of the negatives between all of the elements (the total number of positives and negatives).

Notice that each power expression has more than one solution, when solving the mathematical equations. And this matches perfectly with the result we had from the graphical representation of the negative/positive ratios.

Almost by magic, we have found out that the two representations gives similar results, even though they are based on two completely different philosophies!!  

Amazing, right. But it gets even better in a moment.

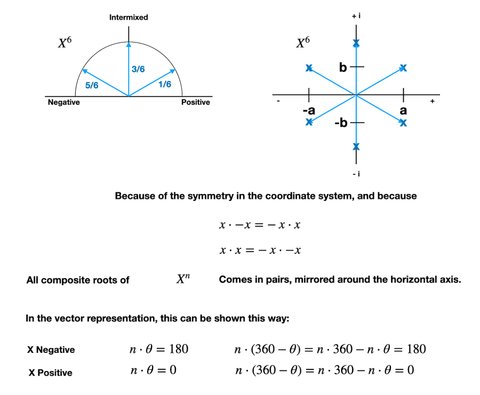
As a result of moving from the "meter representation" of the ratio, to the mathematical equations and the two dimensional coordinate system, something unavoidable happens.

As explained in the illustration, additional roots appear.

So X to the power of 6 now has 6 roots, even though there are only 3 negative/positive ratios possible (the meter representation).

Starting with any of the 6 roots - represented as an a + bi coordinate - you can raise this to the power of 6, and you will get X.      

In the general scenario, X to the power of N has N roots.

In coordinate system lingo, this means that there are N combinations of a + bi that when raised to the power of N will equal X.

Now to the final triumph. Remember that in the example with X to the power of 3, we succeeded in separating |X| from the vector a + bi. And by doing this, we ended up with the situation that the vector has the length = 1. It happens to be true, that regardless of what power N we are talking about, and regardless of whether X is positive or negative, this is always the case.

This opens the door to the realm of trigonometry. Instead of a and b, we can now express the root as an angle theta, and the roots will always be on the perimeter of the unit circle.  And from that finding, the use of complex numbers has spread out to many scientific disciplines, and is in particular now used extensively in physics and engineering.

A final comment. Complex numbers are not an artificial construction. Complex numbers are an implicit part of Math, and Algebra in particular. Complex numbers are not an odd, necessary trick. Complex numbers are the consequence of the Mathematical language, and creates the link between numbers and equations!!  

The take out from all of this is, that all numbers can be viewed as being either a real number, an indeterminate number or a complex number.

If the number is 100% positive or 100% negative, it is called a real number.

If the number is 50/50 negative/positive, it is called an indeterminate number.

If the number has a different negative/positive ratio, is is called a complex number, because it has both a real part and an indeterminate part.

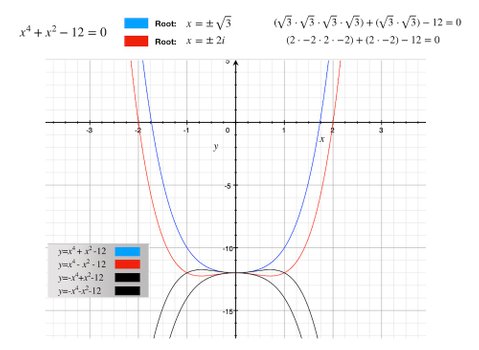
As a final note, the graph shows how this relates to math formulas, graphs and solving equations in general. The example is about finding the roots of the equation in the top left corner. The easy way to find these, is by elaborating on the number of variations the equation can be written by changing the sign of the parts containing X, and then plotting these. The blue solution is straight forward, because the equation to analyze apparently has real roots. The red curve is the result of x times x being negative. And the root = 2 does then mean that the actual root is 2i.   

When using this method, and you end up with a bunch of curves where non of them crosses the x-axis, this means that the equation has no real or indeterminate root - but only complex roots.

Disclaimer: 

In mathematics the indeterminate part is called imaginary.

This is very sad, and the terminology should be changed, because there is nothing imaginary about complex numbers. My advice to you is to think of i as indeterminate, meaning neither 100% positive or 100% negative.

As you can understand from this article, the angle of the complex vector is actually a representation of what should have been called the pn-index (positive-negative index). And when the angle of the vector is 90 degrees, the vector is i, and the pn-index is 50%. And this, as you now understand, means that for each positive x, there is also a negative x. I.e. the amount of positive and negative x is the same. 50% positive, 50% negative.