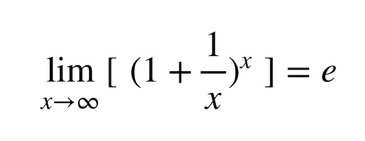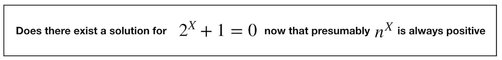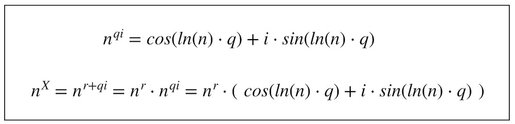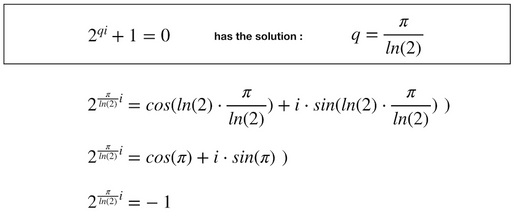Eulers Identity
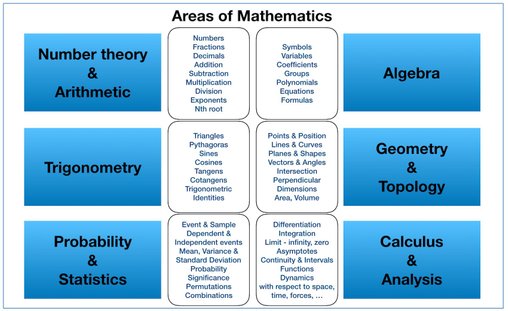
The first place to start, if you want to understand the awe and confusion that this identity lead to, when it emerged, is to get an overview of the different math disciplines.
Arithmetic and Algebra represent the basic building blocks of everything that comes next. Unless you are studying the science of math, there is very little to learn about these two areas, and most likely you know everything you need to know about this already. The only really challenging thing that might give you a headache, is the complex numbers, but that has already been explained thoroughly in another article on straynot.com.
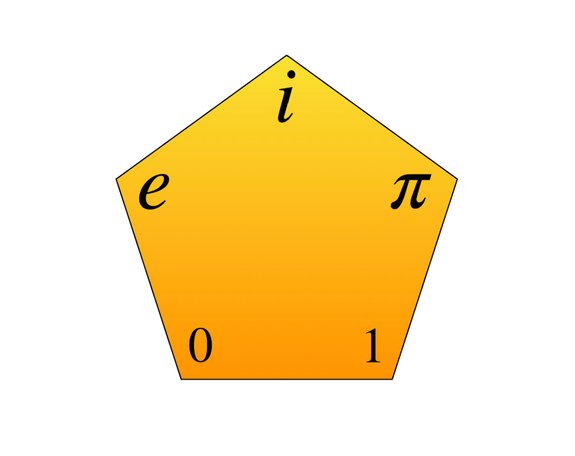
Looking at Euler's identity, the numbers 0, 1 and i stems from these two mathematical areas. And the interesting part here is that there is absolutely no relationship between 1 and i. Stated in mathematical terms, 1 and i are orthogonal - meaning that there is no way what so ever that you, through mathematical operations, can convert 1 to i or vice versa!
Trigonometry is also kind of trivial. If you have heard about Pythagoras, and knows the difference between sin() and cos(), you are probably already mastering this. The real obstacle in this area is about learning by heart all the many identities (different expressions with same result) that has been defined within trigonometry.
Geometry is a different matter. Randomly shaped objects in an arbitrary number of dimensions, that can be moved around, rotated, changed and made calculations on. If you have the need to muscle such objects, you’ll need a computer and dedicated tools that supports this.
Again, looking at Euler's identity, these two areas are the birthplace of pi. Yes sure, pi is "just another number". But pi is a very, very special number. It is the number that represents the ratio between a circles diameter and circumference. Pi is the key to calculating the dimensions, surfaces, areas and volumes of circles and spheres. Pi is most certainly not just an arbitrary number.
Calculus is the most abundantly applied math discipline by far. And second to this, the probability & statistics area.
You will use Calculus and Statistics, when trying to write down formulas that explains various mechanisms in the real world, or when wanting to analyze measurements and observations of the same. Though mentioned here as a pair, as if they are identical and can do the same thing, nothing can be father from the truth. Where Calculus is predominantly focused on continuous systems, and infinitesimal changes, Statistics is rooted in the law of the large numbers, i.e. discrete values and events. Both are extremely potent and have fostered amazing insights and understanding of the world around us.
Looking at the remaining part of the Euler identity, we find the number e, also called Euler's number. Just as was the case with pi, this is no arbitrary number. In fact, e is turning up all over the place, in calculus and in statistics. Intrinsically hidden in the core of continuous evolution, be it growth or decline, you find e. The number e represents the
limit of optimal growth, when the growth is determined as a percentage of the current state, and the percentage pr. time-unit is constant over time. As you might expect - if you know that money in the bank grows faster, the more often interests are added - the greatest growth comes when the number of steps are infinite, which is another way of stating that the fastest growth comes when interest is added continuously. The Euler number is the largest growth factor that can be achieved from 1 percentage of growth, and is achieved by splitting the 1 percentage into infinitesimal small "chunks". The end result will be e times the starting value.
And on top of this, the natural logarithm and the natural exponential function both have some exquisite characteristics when it comes to differentials and integrals. Math equations and expressions becomes more simple and more beautiful, when represented in these "natural" functions. When describing natural, physical phenomena such as a oscillating system that is impacted by a force proportional to the speed of motion (for instance a damping factor), the exponential function becomes the core of the expression describing that system's development in time.
And e is the root of the natural logarithm and the exponential function.
So there you have it. The real numbers zero and 1, the imaginary number i, the key to circles and spheres, and the root of natural, continuous development shares a non-intuitive connection, across the various mathematical disciplines.
It defies reasoning, and yet it is a fact. Because it is a mathematical identity!
Let's discover the explanation for this, in the article below.
THE SURPRISING LINK: A bridge between Arithmetic, Trigonometry, Geometry, Calculus and Statistics
Sometimes when you least expect it, you seem to have discovered a deeper connection between entities that were previously considered to be disconnected. This was the feeling that spread across the mathematical community, when Euler first presented the mathematical expression that is now known as Euler's Identity.
It is called an identity, and not an equation, because you are not calculating anything, and you are not solving any equations. A mathematical identity is simply stating some indisputable and condition-less facts. And in this case it is about the relationship between the numbers zero, one, pi, Euler's constant and the imaginary number i. Essentially, they are all nothing more than numbers. 4 of them real numbers, and one of them non-real (so to speak).
So what's the fuzz ?
The most beautiful Math originates from Complex Numbers
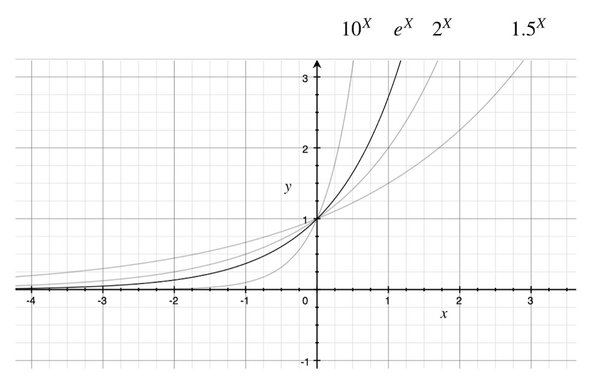
The graphs shown, represents 4 examples of the exponential function, with 4 different values for n: 1.5, 2, 10 and then this strange number called e that we will get back to soon.
What you should notice from these graphs are 2 things. First of all, the function gives positive results for all values of x, from minus infinity to plus infinity. Secondly, you have probably already noticed that all curves shares one single point in the plane. Regardless of what value n has, when x is zero, the result is 1.
With this brief introduction to the exponential functions, the challenge immediately becomes apparent. If all results of n to the power x are positive, then we can write this equation that we would expect will have no solution. But before we just accept this, let's remind ourselves of the surprise - and the joy - we got, when we had a similar, unsolvable expression for the x to the power of n.
So instead of just giving up, let's delve on this for a moment.
What we learned from the first article on complex numbers was, that there is an intrinsic asymmetri in the mathematical language that can only be resolved by introducing complex numbers.
By the introduction of complex numbers, the expression x to the power of n can now have both positive and negative values, regardless of whether n is odd or even.
Of course, this great success inspires us to take aim at another asymmetric mathematical expression, named the exponential equation. In this equation, the roles of x and n has been flipped around, and now we would explain it as n to the power of x .
First we need to understand the basic algorithmic rules for exponential expressions. If the exponent is a sum, then we get the same end result, by multiplying each of the single elements as their own exponential expression.
Ok, now we are ready to introduce the complex numbers.
First, we consider what happens, when X is the complex number r + iq. By use of the rule mentioned above, we find that we end up with a situation where we can treat the real part r, and the imaginary part q, as two separate parts of the equation.
In line with the rule, we can also conclude that n to the power of 2i is the same as two separate expressions, each with n to the power of i.
With all this tedious, but actually very basic math, out of the way, we can now use our learnings from the first article, to get to a clear understanding of what complex numbers offers, when it is being used in the context of exponential expressions.
The remaining part of this article is based on one single assumption - namely that n to the power of i is a complex number. And this shouldn't worry you, because you already know that complex numbers represents all the numbers we know. So this must always be true - even if the number was actually a real number.
Have a look at the illustration with the circle. The vectors are representing the numbers listed on the left side. What we notice is, that when q increases by 1, the angle increases by theta. But before we can find the precise vector coordinates a and b, we need to know the size of theta.
If you are experience with differential equations, you already know that the rate of change - the change in the exponential functions result, when the exponent is changing - is given by the d/dx of the function. And this, combined with the fact that n raised to the power of zero equals 1 (remember the point of the plane that all curves were crossing) gives us the value of theta = ln(n).
Let's recap what we have just learned. n raised to the power of a complex number is equal to a vector. And the angle of this vector is determined solely by n, the base number of the exponential expression. And the larger the value of n, the larger the value of theta.
From the previous article, we learned that these vectors can be represented by the trigonometry functions cos and sin, and the general expression - for arbitrary values of n, q and r - is shown in the illustration.
Again, as was the case with the x to the power of n, we end up with a mathematical expression telling us that two, seemingly unrelated functions - exponentials and trigonometry - share a common foundation.
This equation materialized almost out of the blue, but don't be fooled. This equation has had the most profound impact on math and science, since its discovery.
Remember the curve with the base number e? Let's talk about that now.
The number e = 2.7182818.... is a very special number. When the base n equals e, the tangent to the curve (the d/dx) at any specific point equals the value that e to the power of x has in that specific point. Long story short, what this also means is, that the trigonometry representation of e to the power of x becomes even more simple.
Now listen to this. For a very certain value of q, the equation can be transformed to what has since been called the most beautiful identity in Mathematics.
(notice: it is called an identity, and not an equations, because there are no unknowns, no x).
This identity indicates a relationsship between e, phi and the imaginary number i, in combination with 1 and 0 (both of which, also have very characteristic behaviors).
This identity has been given the name Euler's Identity, in honor of the famous mathematician that first proved this connection.
Knowing what we know now, we will have no trouble solving the equations from previously.
It turns out that yes, the equation has a solution, and the result is as shown.
This brings us to the end of our story about the complex numbers - the numbers that turned out to be real, necessary and the fulcrum of symmetry of the mathematical language.
As a final note, let me just one more time refrain: there is nothing imaginary about complex numbers. My advice to you is to think of i as indeterminate, meaning neither 100% positive or 100% negative.
@Instagram: istraynot
© Copyright. All Rights Reserved.