Modeling the Real World
CONSTRUCTING WHAT ALREADY EXISTS:
In our perception, at least
Why are we so fond of playing with Lego?
Lego offers us the opportunity to engage in activities that stimulates two of the most satisfying moods, and make us thrive - creativity and the ability to succeed. The underlying instincts are of course, the curiosity about the why and the how, and the desire to make something useful out of our knowledge.
I guess we have all heard sayings like:
If you can’t explain it, it’s because you don’t really understand it
If you understand it, you can also draw it
It is important for many people to be able to prove that they have the brains to conceive new constellations and the skills to see it through.
This is why we solve puzzles, play games, write books, engage in adventures, create new businesses and so forth. But it is also the main characteristics of what makes a great scientist or engineer.
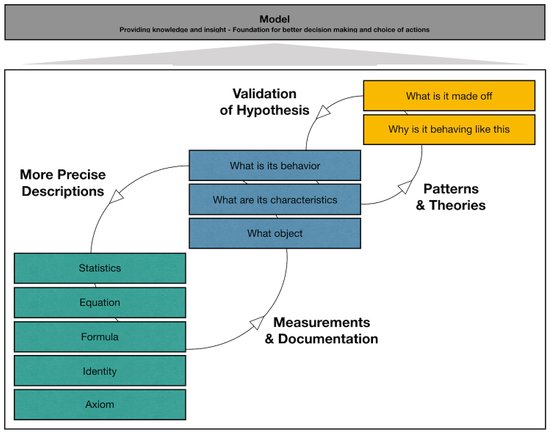
In science, it’s all about the discipline of Scientific Modelling, and producing the scientists blueprint of how it all makes sense. The model becomes the framework for description, understanding, making hypotheses, conceptualizing tests and pinpointing areas to be further elaborated.
By now, after millenniums of scientific struggles and successes, we have conceived models for almost anything that exists in the world around us. For instance, the Natural Sciences have models explaining physical phenomena, chemical reactions, biological physiology, the origin of the continents, atmospheric systems, cell mechanisms and DNA structure. And even the behavior of black holes, more than 50 million lightyears away from the Earth. Imagine that.
Engineers also make models, but they are a slightly different kind of models. As an example, engineers use models to imitate deploying the Explorer on the surface of Mars, long before the transportation rocket has even been sketched. To make proof of concepts, evaluate what-if scenarios, simulate conditions that cannot be reproduced here on earth, and much more.
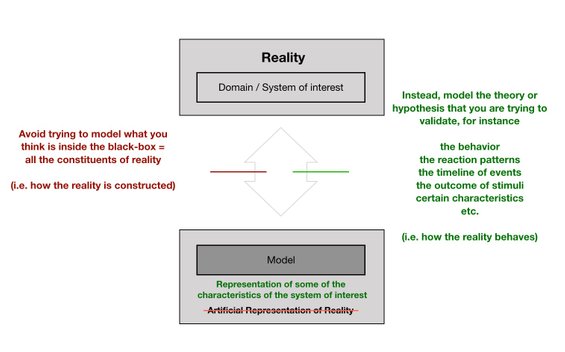
What does a model have to encompass in order to be a good, and acceptable model. And even more importantly: what is the model representing - what is it, in essence, a model of?
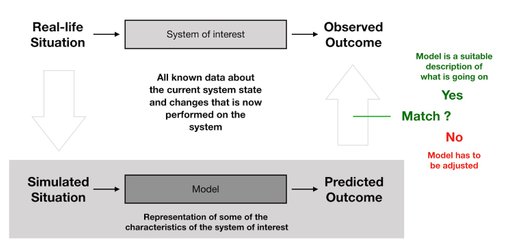
A representation of the world in a box, and looking at the box from the outside, looking in. Trying from what we experience, to deduce its composition and behavior, internal dynamics and responses to external conditions and influences. That is is principle all the model is.
It is important to remember that models are merely abstractions and approximations, and the whole is often greater than the sum of its parts. We might never understand fully what is inside the box. But we need to know what to expect from it - what will come, and how we can influence it in our favor, and get the best out of it.
This is why we model. And we have become damn good at it - thanks to the scientists and engineers.
Modelling the virtual reality
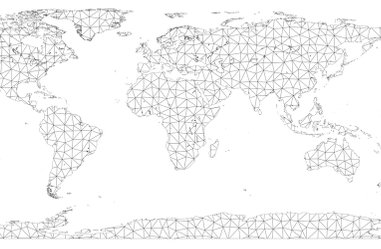
Now we would have to introduce new concepts such as a squeezed, bumpy globe, north, east, latitudes, shores and borders. This could in theory also be managed through the use of math, though at the end, it would still be an imperfect simplification. To succeed, we would have to make approximations and shortcuts.
But how would we describe the destinction between countries, oceans, lakes, mountains, glaciers etc. To describe these, we would have to introduce something more than math.
If you are modelling a map of the world, you need to find a way to translate the concepts of countries, mountains and rivers onto the map model. Just like if you were to model an animal like a tiger, you would first need first to pinpoint the characteristics and patterns that makes a tiger unik, and then have this knowledge represented as part of the model, if the model is to work as expected.
What's in a heartbeat? Can you understand - or even describe - a heartbeat, without having to go into details about a whole lot more than this .... heartbeat. And what would be your point of view. If you are a Radiologist, you most certainly would make a different characterization than a Dietitian would, and both would be completely off, if they were trying to translate their knowledge into what it feels like to be an unborn child inside the mothers womb. And during this story-telling - because that is what you are doing - telling a story about how you, yourself are perceiving it - you would have to have some understanding of how this will be interpreted, at the receivers end.
Common ground, contextual settings, conceptualization, details and language goes hand in hand, when trying to "explain" - or model - something.
It is easy to describe what a "Circle" is, to someone who is already acquainted with this "thing". But when it comes to describing a circle, previous knowledge is not even a prerequisite. We could write down a formula that would "produce" a circle, and through this convey the insight, assisted by the general language of Math.
But then, what about for instance a map of The World?
To understand the distinction between what can and cannot be described through the use of math, let's take another example - an Architects blueprint of a house.
The size of the house and rooms, orientation of the house relative to North and the rooms individual position relative to each other, headroom space, thickness of the walls, etc. - all this can be represented in a mathematical model. The strength of the building materials, the weight, the sound and temperature isolation index, the luminosity of the lamps during the night, the view from the window, the sunlights angle during all seasons of the year etc. If you have ever seen a virtual representation of a house, you would know that there are standard tools to make dynamic, 3D representations that look really authentic. All this is achieved almost purely through the use of mathematics.
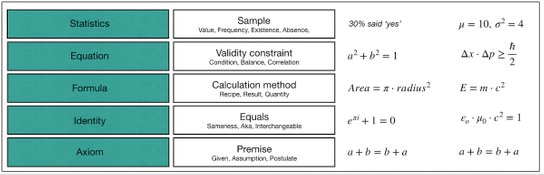
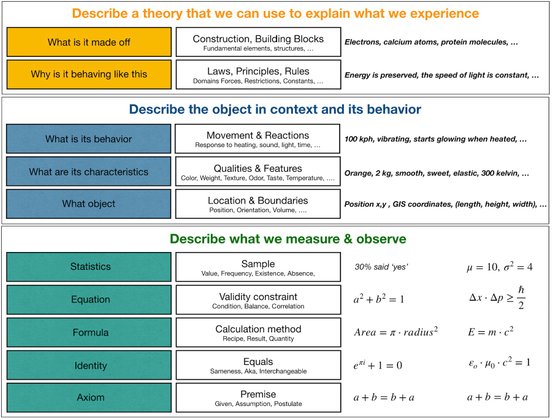
When we say "this can be represented via math", what do we mean ? In general, the math statements used can be categorized into 5 layers. The Axioms are the skeleton of the mathematical language, and everything else builds from this layer. This is the founding layer of rules and definitions. From that, we can deduce a number of identities = aliases and substitution tricks, that we can use, to shift between different expressions of the same fundamental statement. The 'Formula' and 'Equation' layers are the most intuitively understandable usage of math sentences. The formulas can be used to fx. calculate the weight of the windows of the house. And the equations can be used to find out how many watts must be deployed in the lamps of the house, to achieve the desired level of brightness in the kitchen. Finally, we have statistics which has so many applications that it deserves an article of its own (please see the other article on that topic).
In general, if you know the values of the variables that goes in the formulas and equations, and if you can find the correct values of the parameters and constants that constitutes the expression, you can in principle calculate the result to the desired level of precision.
If ... if .... in principle .... That is a lot of if's. So what's the catch?
The first issue is, that it is not everything that fit's nicely into a formula.
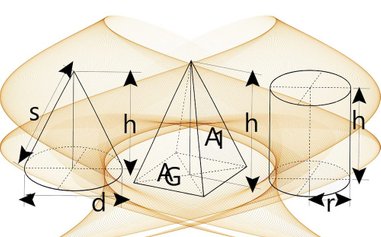
For instance, if you consider shape and volume. The formulas for the volume of a box, cylinder, cone, pyramid etc. are well known, and very simple to use.
But what is the volume of a cloud in the sky? As soon as you come across irregular shapes, the traditional forms fall short. Then if you as the next-best option had a formula for the surface area of the cloud, you would be able to calculate the volume through the use of integrals. But this is somewhat like a chicken and egg problem. You need to know the shape to deduce the formula, or you need to know the formula to deduce the shape. And you can hardly think of anything more volatile than the shape of a cloud, so we would have to come up with another solution.
The only way forward, is to make some approximations. For the sake of the argument, let's decide that we will treat the cloud as having the shape of a cylinder.
Here comes our next problem. Where does the cloud start, and where does it end? Not everything has definit boundaries, and a clear definition of inside and outside.
Remember our World Map from before. We were about to mark the position of mountains and lakes. But where does the hill end, and the mountain start. And what part of the Sea surface belong to the ocean, and what part belong to the rivers and lakes?
We are now at the core of the modelling challenge.
Modelling is somewhat like building an alternate reality with Lego, and then some. In effect, everything that is going to play a role in your model, has to be represented as building blocks. And these building blocks can be math, discrete objects, generalized rules, positions on a grid, events, predefined reactions and patterns etc. And when you model, you have to make a decision on how to represent these building blocks. What are the components, what are their characteristics, where are the boundaries, what is inside, what is allowed, can objects overlap, what happens if they clash etc.
Some of this can be represented by exact mathematical expressions, but some of it needs to be translated into objects, characteristics, behaviors, events, rules etc.
A model is a combination of some aspects which can be formulated through math, and then a more abstract representation describing the context, the objects and their dynamics.
Finally, a model - when we are talking about scientific models - will also include an additional layer, suggesting reasons and explanations for why the objects are behaving and reacting as they are. This is what we refer to as the "theory".
Before we go on, please pay attention to this. Models can vary from being almost 100% mathematical, to being based purely on processing of data input, evaluating the current state and extracting learnings and insight from that. Depending on what science discipline we are talking about, the right split between these two approaches is essential.
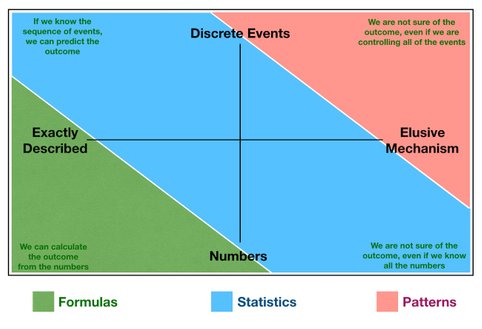
The illustration shows the 4 opposite corners of the modelling playing field. The 4 textual representations mentioned in the illustration are just mentioned here, to indicate the key differences of the 4 quadrants. There is an endless amount of applications of each of the 4 types.
The Colors indicates the methods and models used to decipher and describe real-life complexities, dependent on the domain, number of variables and number of objects.
And sometimes the model you need to implement, must handle a combination of 2 or more of the individual types, and therefore must handle both the formulas, the statistics and the pattern matching, in combination.
Except for the upper right corner, based solely on events, states, rules and pattern matching, the remaining part of the modelling solutions will be processing numbers, so let's focus on those, for the remainder of this article. Don't get me wrong, pattern matching also requires a whole lot of processing, it's just a different type of processing. This is extensively exploited in the AI and Machine Learning community. To briefly explain the distinction here, let us just take a very simple example - salary calculation - using a "processing methodology" invented in the early days of Machine Learning.
In most situations, there is a delicate matter that must be resolved before a mathematician can write down the exact formulas and equations needed. And that is to know all the relevant dimensions of the model - and thus the variables that should be introduced as parts of the mathematical formulas and equations.
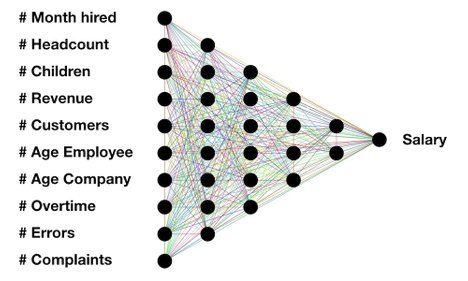
To understand what is meant by "dimensions", let us have a look at a simple example. Imagine that you are a CFO of a company, and want to develop an easy formula for calculation of the salary of each of the employees. Your concern is that it has to fair, in the sense that alike employees should have similar salaries. But you just don't know what constitutes the defining characteristics of "alike employees".
Of course you could decide that all employees should have exactly the same salary, and then everything would be easy - from a modelling point of view. This is the scenario shown in the illustration, where the number of dimensions equals zero = no variables involved.
The more variables you introduce into your formula, the higher number of dimensions goes into the calculation. But notice that in order for it to be a dimension on its own, it has to be orthogonal to - meaning independent of - the other variables. That is to say - if you were to put both "month" and "years" in your equation, these would not represent two different dimensions, obviously, because the one can be calculated from the other.
It is important that you understand this concept, when we start looking at the other science disciplines. When you are presented with something said to be a 10-dimensional space, what this means is, that there are 10 independent variables that goes into calculating the outcome. It doesn't mean "spacial dimensions" in a geometric (volume and surface) sense!
One more thing to notice, concerning this multidimensional solution space. Let's say we had a 10-dimensional Salary Calculation formula. Even if - for two different employees - all the 10 variables were different for the two employees, they could still end up having the same Salary. So in a 10 dimensional space, there could be many "points" in that space that resulted in exactly the same outcome (salary). Like in the 3 dimensional space that surrounds you, right now, the air temperature will probably be the same, in most of the "points in the 3 dimensional space", even though the points all have their own, unique coordinates x,y,z.
If the mathematician has a hard time deducing the optimal (fair?) equation for salary calculation, there exists an alternative way.
Have a look at the illustration with the 10-dimensional Salary calculator. This picture illustrates a different type of "calculator", based on what is called a neural network. This represents a completely different way of implementing the "model", where you "configure" the model, instead of entering math formulas or rules.
The way this is being done practically, is by feeding the model with various combinations of the 10 dimension input together with the "expected" salary result. In reality, the neural network is being trained and taught on how to react in various situations.
This method requires a lot of preexisting data sets - combinations of the 10 variables and the corresponding expected salary, and the usage in this example is maybe a bit speculative. But in fact, this method is being used extensively, in areas where the desired "model" is hard, or maybe even impossible to define or settle on.
When the model = the neural network has achieved the necessary level of training, the model will be able to give salary answers for combinations of inputs that it has never met before, and never been trained for. That is to say, that the model can now answer what is the fair salary for all combinations of the 10 dimensional input.
And the use of such neural network based solutions can often be implemented with impressive results.
The fascinating point here - and what should be your takeaway from this - is that even though there is no math formula to be found in the core of this model, the result is still deterministic. There is no randomness at play here. The effect simply stems from a number of "autonomous objects" (the nodes in the network) adjusting themselves to the circumstances presented to them - the input parameters and the expected result.
Spend a moment to digest this insight. That observations that we make in our daily lives, can originate from a deterministic "mechanism", even though this mechanism cannot be translated into a mathematical formular.
We intuitively accept this, when we are arguing that we cannot track all air molecules in a room simultaneously, but still can agree that the air temperature is determined by the laws of physics - i.e. a mathematical description. But actually it is the same situation that is happening here. The air molecules movements are determined by the "circumstances presented" to the air molecules, i.e. the volumen of the available space, the pressure from the boundaries of that space and the total energi shared among the air molecules. No one - and I mean no one - can provide a formula for the exact position and movement of the all of the individual molecules. Instead, this is being described by the use of Statistical Mechanics. So we end up with a number of formulas - describing the "end result" or the outcome - but we have no formula for describing the constituent parts.
This is the heart of Science. Scientists are driven by the desire to explain what we observe and why it is so. Through theories and models, scientist are able to use this insight to make predictions and suggest actions that will benefit the world and its population.
Only in very few areas, are the scientists trying to track - and model - all the constituent parts. Most often, the science is describing the effects of a huge number of "components" acting together and influencing each other - using statistics, pattern matching and other types of number crunching.
This brings us back to the questions about the World Map and the Clouds.
Science doesn't have to model the exact geography and physical representations, to teach us a whole lot of important knowledge about the Countries and their populations, the Mountains, the Sea and the Sky. For instance, the exact shape of a cloud is irrelevant, when you study the Water Cycle and the factors that influences precipitation patterns around the world.
Models are made with the purpose of providing results such as answers, insight and forecast. And the model should be designed accordingly, with this purpose in mind. Number precision, Dimensions, Math versus Rules and so forth should be chosen exactly to suit the purpose, and nothing more than that.
Except for the very simple and straight forward examples, models are always approximations of a real-life situation. Or sometimes the opposite way around - the model will dictate the implementation of the model into the reality, adapting the results in daily situations and decision making (like in the case of the salary calculator).
In many situations, modelling is a cognitive process. Your personal understanding about the things you are looking for - and trying to figure out via your model - will unavoidably influence the way you construct your model. And all these "pre-modelling" considerations and decisions, will dictate the solution space, and eventually the end result. A priori conceived concepts, rules and state of mind affect the questions you are putting forward, and the method you are using, trying to answer those questions.
Modelling is not math, and math is not a model. Part of the model might end up being math equations, but modelling is about using math in a certain context, under certain conditions, and deciding on how to translate the input and the result back to a usage scenario and an outcome. And the usage scenarios and the models will be completely different, dependent on the science domain, and dependent on what the scientist is trying to prove. The same basic formula can have many applications. Take for instance the exponential function. The usage and interpretation of the results, will be very different in finance, biology, physics and engineering. These will be represented by completely different models, even though all models might "predict" some kind of exponential rate of change.
The scientific model can be viewed as consisting of 3 layers: the numbers and formulas, the object model and the theory. The first two layers represents the facts; stuff that can be measured, things that can be observed. The third layer represents the scientific theory that we use to explain the reason behind all this.
The measurements can always be more precise, and the formulas used, often be improved. Then the object model will improve, and maybe even change considerably, when more precise measurements are presented. And new insight often also provokes the need for adjustment of the previously used theory, into an even better explanation.
This is the scientific method at its core. The continuous construction of models and theories from facts, repeatedly refining the measurements and the formulas, reconstructing the model and scrutinizing whether the theory is acceptable - a perpetual search for more facts, more insight and the perfect theory that can explain all that we currently know.
Always remember this. A scientific model represents a perspective on the reality - not The Reality.
Having said that, we have to acknowledge that the Scientists and Engineers have been extremely successful in implementing and using models.
Before closing this topic, let me make a final comment about modeling the various phenomena of the world. There are two distinctly different traits and at play here, that requires two completely different approaches and skillsets.
It all comes down to the difference between static systems and dynamic systems.
In the descriptions above, we have primarilly been focusing on static systems, meaning systems structure, composition and characteristics as such, static in time and without motion of any kind.
In the article "Simulation and Reality", we will look at what it takes to succeed with simulating dynamic systems, and what to be aware of with regard to that.
@Instagram: istraynot
© Copyright. All Rights Reserved.